Wolfram|Alpha
un moteur de requètes pour
le calcul scientifique
Table des matières
1. Qu’est-ce que Wolfram|Alpha ?
2. Les premiers pas...
3. Exemples.
Questions.
1. Qu’est-ce que Wolfram|Alpha....
→ un site internet sur lequel on peut poser des questions et résoudre des problèmes dans une multitude de domaines, en particulier en mathématiques...
→ la syntaxe des requètes est en format libre.
C’est à dire qu’on écrit sans avoir à respecter des règles de syntaxe particulières. Cependant......
.....les questions et les réponses s’écrivent en anglais !
→ Pour utiliser Wolfram|Alpha depuis n’importe quel navigateur connecté à l’internet, il suffit de se rendre sur le site :
![]()
→ Wolfram|Alpha est basé sur :
– un système d'interprétation du langage naturel (les requètes...),
– une unité de calcul dynamique,
– des bases de données traitées et mises à jour par Wolfram Research.
Tous les calculs sont gérés via Mathematica sur les serveurs de calcul très puissants de Wolfram Research :
● ~![]() opérations mathématiques traitées par seconde,
opérations mathématiques traitées par seconde,
● plusieurs milliers de processeurs dernier cri,
● 65 Gbytes de RAM,
● plusieurs Terabytes de mémoire...
Ce qu'en dit Steven Wolfram :
"− vous n’avez pas à employer de syntaxe précise dans Wolfram|Alpha, vous pouvez écrire des requêtes comme vous y pensez, en format libre et en anglais.
Wolfram|Alpha essaye alors d’interpréter votre demande et la transforme en instruction précise du langage Mathematica, puis l’exécute.
− sous leurs formes natives, Wolfram|Alpha et Mathematica fonctionnent de manières très différentes. Wolfram|Alpha accepte des requêtes en format libre, par contre Mathematica exige l’utilisation de son langage formel précis. Il permet de construire des programmes et des calculs de complexité arbitraire. Ce qui est formidable c'est que ces deux approches ont été rassemblées pour produire le meilleur de ces deux concepts."
2. Les premiers pas....
entrez la requète suivante dans la page internet de WA :

remarquez le style utilisé dans la requète...
Entrez maintenant la requète suivante de décomposition en éléments simples :

WA affiche le résultat de la décomposition en éléments simples de la fonction ![]() ···
···
Si vous cliquez sur “show steps” à droite, il vous montre même les détails du calcul :

on reviendra sur cet exemple plus tard...
quelques faits...
WA est plus efficace que n’importe quelle calculatrice de site Web pour résoudre des problèmes de mathématiques (comme celles de Google ou autres...) . Il fournit en plus des graphiques de qualité.
WA gère d’innombrables catégories de requètes : mathématiques, probabilité, statistique et analyse de données, physique, climat, santé, médecine, astronomie, culture, etc... Il contient plus de 10 milliards d’informations, plus de 50000 types d’algorithmes et de modèles couvrant plus de 1000 domaines ! Le projet de Wolfram|Alpha est de rendre accessible un volume toujours plus important de connaissances.
premiers exemples généraux...
entrez les commandes suivantes dans WA et étudiez les réponses fournies :
• Hello
• How can you help me?
• Weather Toulon
• 310€ - 10%
• Hemoglobin
• Next solar eclipse
• highest mountain in the world?
• oldest man in the world?
Publicité.
Comme vous avez pu le constater, WA affiche parfois une fenêtre demandant d’acheter la vesion pro de l’application (3€/mois pour un étudiant...). Fermez cette fenêtre en cliquant en bas à droite (voir figure).
La version pro de Wolfram|Alpha fourni, entre autres, plus d’interactivité sur les graphiques...

Inscription.
Par contre, il est intéressant de s’enregistrer... Cliquez sur le menu “sign in” en haut à droite de la page de WA:

puis remplissez le formulaire (e-mail personnel, mot de passe) et cliquez sur “Create an Account”...
![]()
le fait de s’être enregistré permet d’accéder aux commandes Mathematica que Wolfram|Alpha exécute pour répondre aux requêtes. Exemple :
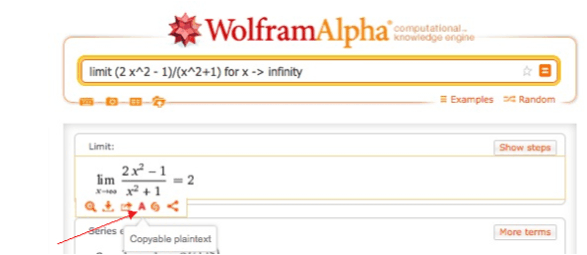
Si vous cliquez sur le symbole “A” de la barre de menu, le texte de la commande exécutée s’affiche :
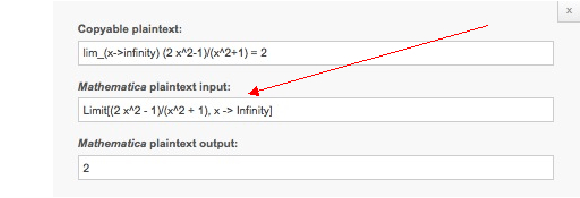
il suffit de “Copier/Coller” ce texte (Mathematica plaintext input) pour sauvegarder la commande...
On a aussi le texte correspondant au résultat (Mathematica plaintext output), ici égal à 2.
![]()
3. Exemples.
Voici d’autres exemples plus intéressants pour nous... testez-les.
• x*x
• solve x^2+2*x-3=0
• solve x^2+1 =0
• solve x+y<1 and y>x (* résolution d’inéquations *)
• plot sin(x^2)
• limit (3x^2-4)/(4x^2+2) for x->Infinity
• derivative of x^4 sin x
• integrate x^4 sin(x) dx
• sin(pi/88)
• 0.03569233383898 ? (* identification fonctionnelle... *)
• log base 2 of (x^2+x)
• slope of the tangent line to x^2 at -1
• addition formula sin x
• discontinuities of 1/x
• P && (Q || R) (* && et || sont les opérateurs logiques: ET , OU *)
• truth table not p or q (* table de vérité *)
• truth table not p or q, p => q
• (A union B) intersect C (* diagramme de Venn *)
• (complement S) intersect (A union B)
• y’(t) + y(t) = 1, y(0)=3 (* équation différentielle linéaire du 1er ordre *)
Vous pouvez aussi explorez les innombrables exemples se trouvant sur le site de Wolfram|Alpha :
![]()
![]()
Questions.
Les questions suivantes sont à résoudre dans Wolfram|Alpha.
Sauvez les résultats contenant vos réponses (Mathematica plaintext output) dans un fichier texte...
Pour les graphiques, sauvez l’instruction Mathematica correspondante (Mathematica plaintext input).
1. calculez les racines de l’équation 3 x^2 - 8 x + 2 = 0
2. calculez les racines de l’équation 3 x^2 + 2 = 0
3. tracez la fonction de la variable réelle x : exp(- 2 x) sin(3 x)
4. résoudre l’équation: exp(- 2 x) sin(3 x) = 0 et vérifier que π/3 est une racine.
5. calculez ![]() (x^2+1)/(3 x^2 - 1)
(x^2+1)/(3 x^2 - 1)
6. calculez la dérivée de la fonction (x^2+1)/(3 x^2 - 1). Analyser les étapes du calcul.
7. calculez la pente de la tangente de la fonction x^3/3 en x=-1.
est-il facile de prévoir le résultat ?
8. calculez l’intégrale indéfinie de la fonction x^2 sin(x). Quelle est la valeur de cette intégrale en x=![]() ?
?
9. résoudre l’équation différentielle: y’(t) - 2 t = 1, y(0)=1.
10. affichez les tables de vérité des 2 propositions: q => p et p => q.
Dans quels cas a-t-on équivalence ? Aidez-vous de Wolfram|Alpha...