Les 2 racines réelles sont calculées et représentées par 2 points rouges dans le tracé graphique de la fonction.
Wolfram|Alpha
Remarque générale. Une fois connecté au site de Wolfram|Alpha -> http://www.wolframalpha.com/ on peut soumettre une question en anglais (consultez le glossaire pour les commandes principales). Les questions posées peuvent être assez générales et couvrent un large domaine des thématiques de l'enseignement scientifique.
Une fois la question correctement interprétée par Wolfram|Alpha, une réponse assez détaillée est fournie avec parfois le détail du calcul effectué...
Questions.
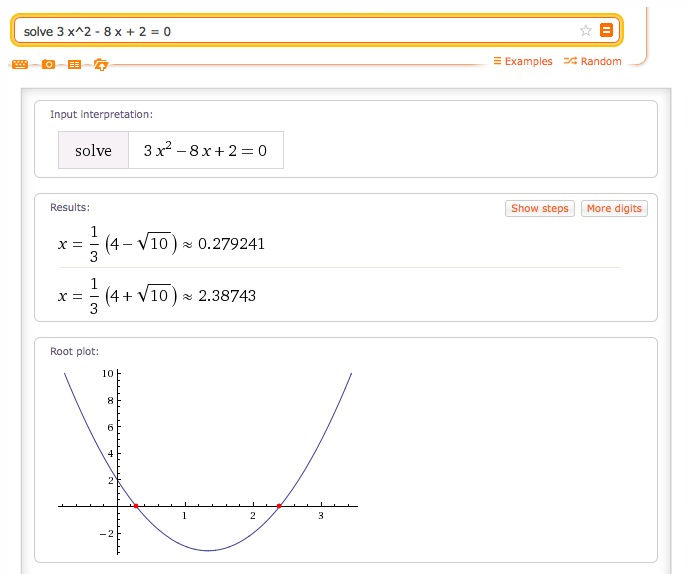
1. calculez les racines de l’équation 3 x^2 - 8 x + 2 = 0
Les 2 racines réelles sont calculées et représentées par 2 points rouges dans le tracé graphique de la fonction.
2. calculez les racines de l’équation 3 x^2 + 2 = 0
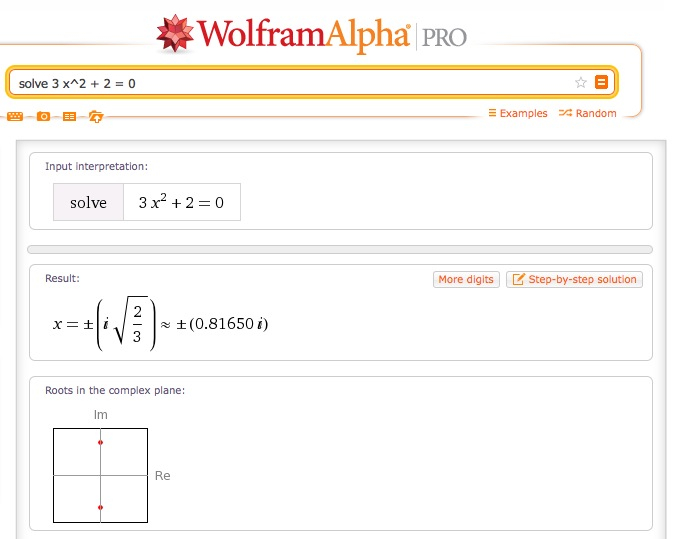
Les 2 racines imaginaires, complexes conjuguées, sont calculées et représentées dans le plan complexe.
3. tracez la fonction de la variable réelle x : exp(- 2 x) sin(3 x)
 sin(3x).jpg)
4. résoudre l’équation: exp(- 2 x) sin(3 x) = 0 et vérifier que π/3 est une racine.
 sin(3x) = 0.jpg)
En faisant n=0 dans le deuxième ensemble de solutions, on vérifie bien que π/3 est une racine...
5. calculez 
(x^2+1)/(3 x^2 - 1)
 sur (3 x^2-1).jpg)
En cliquant sur "Show Steps", les étapes du calcul sont affichées...
6. calculez la dérivée de la fonction (x^2+1)/(3 x^2 - 1). Analyser les étapes du calcul.
 sur (3x^2-1).jpg)
La fonction dérivée est représentée. Si on clique sur "Show Steps", on obtient les détails du calcul...
7. Calculez la pente de la tangente de la fonction x^3/3 en x=-1.
Est-il facile de prévoir le résultat ?
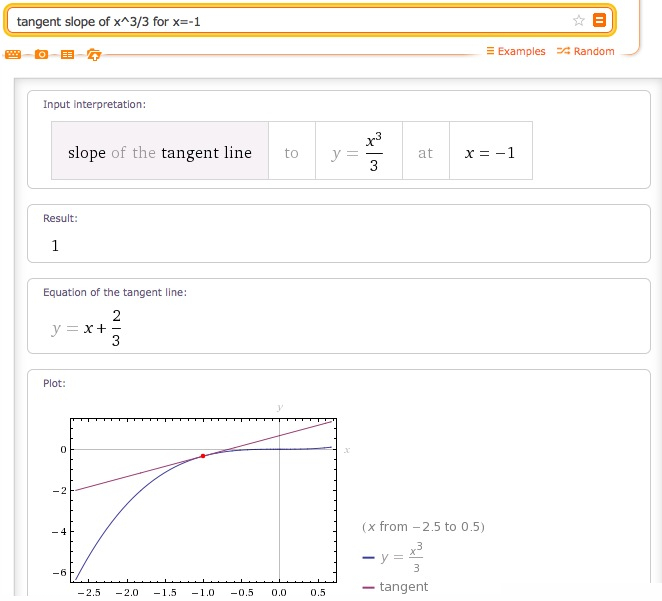
La dérivée de la fonction x^3/3 est x^2, qui est égale à 1 si x=-1. C'est la pente de la tangente en x=-1.
Pour l'équation de la tangente, on vérifie facilement que la droite d'équation y=ax+b de pente 1 passant par le point (-1,-1/3) est y=x+2/3...
8. calculez l’intégrale indéfinie de la fonction x^2 sin(x). Quelle est la valeur de cette intégrale en x=
?
.jpg)
Lorsque x= l'intégrale indéfinie est égale à π + constante (vérifiez-le sur le résultat trouvé par Wolfram-Alpa).
La représentation graphique de l'intégrale correspond à une valeur nulle de la constante d'intégration.
9. résoudre l’équation différentielle: y’(t) - 2 t = 1, y(0)=1.
-2t=1, y(0)=1.jpg)
En dérivant la solution y(t)=t^2+t+1 trouvée par Wolfram-Alpha, il est facile de vérifier qu'on a bien une solution de l'équation différentielle. De plus, si t=0, on retrouve bien la condition initiale y(0)=1.
10. affichez les tables de vérité des 2 propositions: q => p et p => q. Dans quels cas a-t-on équivalence ? Aidez-vous de Wolfram|Alpha...
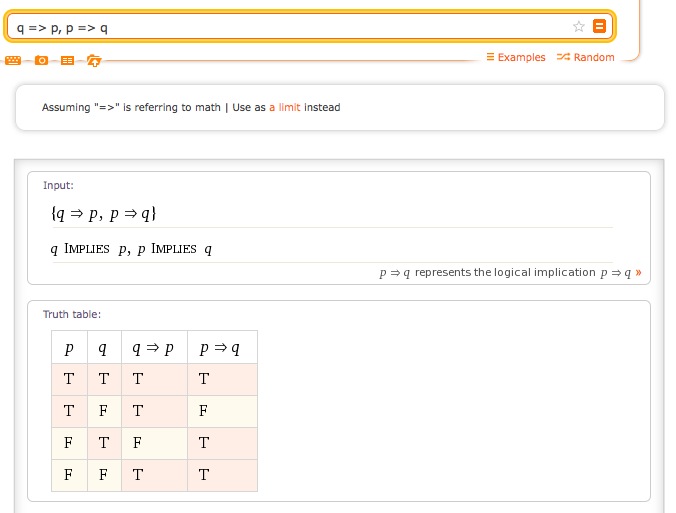
On remarque que les 2 propositions sont équivalentes si p et q sont vraies simultanément ou bien fausses simultanément.
